Magnetic Field

Consider an isolated magnetic pole placed at any point. It experiences no force. When another magnetic pole is placed near it, a force starts acting on it. For the first pole, the properties of space around it have undergone a change due to placing of the second pole near it. This space, with modified properties, is called the magnetic field of the second pole. 

Magnetic field, of any magnetic pole, is the region (space) around it in which its magnetic influence can be realised. 

The magnetic field which we plot, in laboratory, is actually a section of magnetic field in the horizontal plane (paper). 

Lines of Force - "Flux Lines"

Imagine a unit magnetic north pole to be situated at any point in a magnetic field. It experiences a force given by Coulomb's law. If the north pole were completely free to move under the action of this force, it would move along a path called lines of force. 

     Lines of force is the path along which a unit north pole would move if it were free to do so. 

     In case of isolated magnetic poles the lines of force is a straight line while in case of a combination of poles (a magnet) it is a curved line. The arrow head on the line indicates the direction of motion of the free north pole. 

Properties of magnetic lines of force

(i) Lines of force are directed away from a north pole and are directed towards a south pole. A line of force starts from a north and ends at a south pole if they are isolated poles. 

(ii) Tangent, at any point, to the magnetic line of force gives the direction of magnetic intensity at the point [Fig. 1].

Fig. 1. Direction of magnetic intensity at a point. 

(iii) Two lines of force never cross each other. If the two lines were to cross, two tangents could be drawn to the line of force at the common point [Fig. 2] meaning thereby two directions of magnetic intensity at that point, which is obviously not possible. 

Fig. 2. Two directions of magnetic intensity at a point. 

(iv) The number of lines of force per unit area (area being perpendicular to lines) is proportional to magnitude of strength of field (magnetic intensity) at that point. Thus, more concentration of lines represents stronger magnetic field. 

(v) The lines of force tends to contract longitudinally or lengthwise i.e., they possess longitudinal strain as shown in [Fig. 3(i)]. Due to this property the two unlike poles attract each other. 

Fig. 3. Magnetic lines of force. 

(vi) The lines of force tends to exert lateral (sideways) pressure, i.e., they repel each other laterally. This explains the repulsion between two similar poles [Fig. 3(ii)].

(vii) 4π lines of force starts from a unit magnetic pole. 

Representation of Magnetic Field

A magnetic field can be represented by a set of magnetic lines of force. If the lines are spaced widely apart, it is a weak field. If the lines are situated close to each other, it represents a strong field. A magnetic field is of two types. 

     (i) Uniform field. A magnetic field is said to be uniform if it has same strength in magnitude and direction at all the points. It represented by a set of parallel lines of force. 

     [Fig. 4(i)] represents a uniform field directed from left to right. [Fig. 4(ii) and (iii)] represents uniform magnetic field at right angles to the plane of the paper directed outwards and inwards respectively. 

Fig. 4. Representation of uniform field. 

     (ii) Non-uniform field. A magnetic field is said to be non-uniform if it has different field strength at different points. It is represented by a set of convergent [Fig. 5(i)] or divergent lines of force [Fig. 5(ii)].

Fig. 5. Non-uniform magnetic field. 

Strength of Magnetic Field : (B) (rightwards arrow) 

The strength of magnetic field, which is a vector quantity, can be defined in any of the following ways:

     (i) In terms of force on a unit north pole

     Strength of magnetic field or magnetic intensity at any point, is defined as the force experienced by a unit north pole placed at that point. The direction of magnetic intensity is the direction in which the unit north pole would move if it were free to do so. 

∴            B = μ₀/4π × m × 1/r² = μ₀/4π × m/r²

Where m is pole strength of source. 

Its unit is NA-1m-1 . 

     (ii) In terms of lines of flux. Magnetic flux density

     We know that a strong field is represented by lines of force crowded together. So, crowding of lines of force can also be used as a measure of field strength. 

     Strength of magnetic field at any point, is defined as the number of flux lines passing through a unit area placed normally to the flux lines at that point. 

           B = magnetic flux/area

     This concept leads to the unit of magnetic flux density as 'Wb m-2' also known as 'tesla' in S.I. and Maxwell cm-2 (known as gauss) in C.G.S. system. 

     (iii) In terms of force on a moving charge. When a charge 'q' moves in a uniform magnetic field of strength B, it experiences a force F (rightwards arrow) , whose magnitude and direction is given by the relation. 

           F = qv B sin θ 

Where 'θ' is the angle which the direction of motion of charge makes with the direction of lines of force of magnetic field. 

∴           B = F/q v sin θ

∴     if q = 1 , v = 1 and sin θ = 1 i.e., θ = 90°

     Thus, strength of magnetic field is numerically equal to the force experienced by a unit charge, moving with a unit velocity at right angles to the direction of lines of force of the field. 

Magnetic Field Intensity Due To A Bar Magnet In Free Space

Case (i) Point situated on the axial line End-on position/Tan A position of gauss

     Consider a point P situated on the axial line, at a distance r from the centre O of the magnet of magnetic length  '2l' [Fig. 6].

Magnetic intensity at Practice due to N-pole only, 

         FN = μ₀/4π × m/NP² along NP produced

or     FN = μ₀/4π × m/(r - l)² along NP produced  

Intensity at Practice due to S-pole, 

         FS = μ₀/4π × m/SP² along SP = μ₀/4π × m/(r + l)² along PS 

If 'F' is the resultant magnetic intensity at Practice due to the magnet, 

     F = FN - FS along NP produced

     F = μ₀/4π [m/(r - l)² - m/(r + l)²] along NP produced

         F = μ₀/4π × m [1/(r - l)² - 1/(r + l)²] along NP produced

or     F = μ₀/4π × m [(r + l)² - (r - l)²/(r² - l²)²] along NP produced

or     F = μ₀/4π × m × 4lr/4π (r² - l²)² along NP produced

or     F = μ₀/4π × 2Mr/(r² - l²)² along NP produced

where M = 2 ml is the magnetic moment of the magnet. 

Fig. 6. Field on the axial line. 

In case of magnetic dipole, the two poles N and S are situated very close to each other. Neglecting l as compared to r. 

          F = μ₀/4π × 2Mr/r⁴ along direction of M

or      F = μ₀/4π × 2M/r³ along direction of M

It is clear that the direction of intensity is along the axial line directed away from the centre if the point is situated on the side of N-pole. 

Case (ii) Point situated on equatorial line Broad side-on position/Tan B position of gauss 

Consider a point P situated, on the equatorial line at a distance r from the centre of a magnet of magnetic length 2l [Fig. 7]. 

Fig. 7. Field on the equatorial line. 

Join NP and SP. 

            NP = SP = √r² + l²

A unit north Pole placed at P (to determine the magnetic intensity at P) experiences a force along PK due to N-pole and along PS due to S-pole. 

Magnetic intensity FN at P due to N-pole only, 

         FN = μ₀/4π × m/(NP)² along PK

or     FN = μ₀/4π × m/r² + l² along PK

Magnetic intensity FS at P due to S-pole only, 

           FS = μ₀/4π × m/SP² along PS

or       FS = μ₀/4π × m/r² + l² along PS

Resolving FN and FS along PX and PY. 

Components of F₁ 

        (i) FN cos θ = μ₀/4π × m/r² + l² cos θ along PX

       (ii) FN sin θ = μ₀/4π × m/r² + l² sin θ along PY

Components of F₂

       (i) FS cos θ = μ₀/4π × m/r² + l² cos θ along PX

      (ii) FS sin θ = μ₀/4π × m/r² + l² sin θ along PO. 

Components FN sin θ along PY and FS sin θ along PO, being equal and opposite cancel each other while FN cos θ and FS cos θ along PX sum up together to give the resultant intensity F at Practice. 

         F = (FN cos θ + FS cos θ) along PX

or     F = [μ₀/4π × m/r² + l² cos θ + μ₀/4π × m/r² + l² cos θ] along PX

or     F = μ₀/4π × 2m/(r² + l²) cos θ along PX

From ΔOSP, cos θ = OS/SP = l/√r² + l²

Substituting for cos θ, we get

         F = μ₀/4π × 2m/(r² + l²) × l/√r² + l² along PX

or     F = μ₀/4π × M/(r² + l²)3/2  along PX

where M = 2 ml is the magnetic moment of the magnet. 

In case of a magnetic dipole, two poles N and S are situated very close to each other. Neglecting l as compared to r, 

∴            F = μ₀/4π × M/r³ along PX

Case (iii) Point situated anywhere

Let People be a point lying at a distance 'r' from the centre of a short magnet NS (magnetic dipole), such that the line joining P with the centre O subtends an angle θ with the axial line [Fig. 8].

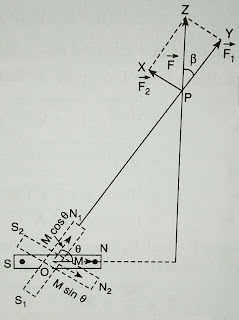Fig. 8. Magnetic field at any point. 

Magnetic moment of the dipole is a vector quantity and is directed along SN. Resolving it into two rectangular components. 

     (i) M cos θ  along OP. 

    (ii) M sin θ perpendicular to OP

Thus, the magnetic dipole can be considered to be equivalent the two magnetic dipoles of moments M cos θ and M sin θ placed perpendicular to each other. 

Point P lies on the axial of dipole of magnetic moment M cos θ. 

Therefore, the magnetic intensity Fax due to this component is

          Fax = μ₀/4π × 2M cos θ/r³ along PY

Point P lies on the equatorial line of dipole of moment M sin θ. 

Therefore, intensity Feq  at P due to this component is

Feq = μ₀/4π × M sin θ/r³ along PX

Since intensities Fax and Feq acting along PY and PX are mutually perpendicular to each other, net intensity F and P is given by

F = √F²ax + F²eq along PZ

or F = μ₀/4π √(2M cos θ/r³)² + (M sin θ/r³)² along PZ

         F = μ₀/4π M/r³ √sin² θ + 4 cos² θ along PZ

F = μ₀/4π M/r³ √sin² θ + cos² θ + 3 cos² θ along PZ

or F = μ₀/4π M/r³ √1 + 3 cos² θ along PZ ... (1)

Direction. In triangle PYZ,

tan β = ZY/PY = M sin θ/r³ × r³/ 2M cos θ

or tan β = 1/2 tan θ ... (2)

Special cases:

(a) If θ = 0, i.e., P lies on axial line.

Using equation (1) and (2), we get

F = μ₀/4π M/r³ √1 + 3 cos² θ along direction of M

F = μ₀/4π × M/r³ along direction of M

and tan β = 1/2 sin θ = 0

i.e., β = 0

The result agrees with that as obtained earlier.

(b) If θ = 90°, i.e., the point lies on equatorial line.

Using equation (1) and (2), we get

F = μ₀/4π M/r³ √1 + 3 cos² 90° along direction opposite to M

F = μ₀/4π M/r³ along direction opposite to M

tan β = 1/2 tan 90° = ∝ i.e., β = 90°

Direction of F will be at right angles to the equatorial line. This result also agrees with that obtained earlier.

Important Notes:

1. Direction of magnetic intensity at any point, on the axial line of a bar magnet is always parallel to the direction of its magnetic moment vector.
2. Direction magnetic intensity at any point, on the equatorial line of a bar magnet is always anti-parallel to the direction of magnetic moment vector.