Kirchhoff's Law for Electrical Networks:
First law :
It states that the algebraic sum of currents meeting at a point is zero.
This law may be called Kirchhoff's current law (KCL).
To explain this law consider a number of wires connected at a point P. Currents i₁, i₂, i₃, i₄ and i₅ flow through these wires in the directions as shown in Fig. 1.
 |
| Fig. 1. Currents meeting at a point. |
To determine their algebraic sum of electric currents, we follow the following sign conventions.
- The currents approaching a given point are taken as positive.
- The current leaving the given point are taken as negative.
According to kirchhoff's first law,
i₁ + i₂ - i₃ - i₄- i₅ = 0 or ∑i = 0
The most evident conclusion of this law is that the current entering a point must be the same as that leaving it. Hence, there cannot be any accumulation of charge at any point in a conductor. This is in accordance with law of convention of charge.
Second law :
It states that in a closes electric circuit, the algebraic sum of e.m.f. is equal to the algebraic sum of the products of the resistances and the currents flowing through them.
This law may be called kirchhoff's voltage law (KVL). It is in accordance with the law of conservation of energy.
Fig. 2. Shows a closed electric circuit.
 |
| Fig. 2. A closed electric circuit. |
ABCD containing resistances r₁, r₂, r₃, r₄ and r₅ in the parts AB, BC, CD, DA and AC respectively. Also, let i₁, i₂, i₃, i₄ and i₅, be the respective currents flowing in these parts in the directions shown by arrow heads. Two sources of e.m.f's. E₁ and E₂ are also connected in the mesh.
In order to use kirchhoff's voltage we shall follow the following sign conventions.
(1) If the electric current flows through the electrolyte of the cell from negative to positive terminal [Fig. 3(i)] the e.m.f.of the cell is taken as positive (+E). |
| Fig. 3. Sign conventions for source of e.m.f. |
(3) If the path taken to traverse the resistance is along the direction of current [below Fig. 4(i)], the final point (B) is at a lower potential than the initial point (A). The product of current and resistance in this case is taken as negative (-ir).
 |
| Fig. 4. Sign convention for 'ir'. |
Important notes :
- From kirchhoff's current law it can be concluded that the potential at any point, in an electric circuit, remains constant whatever may be the number of wires connected at it.
- Kirchhoff's voltage law, may be seen as the generalisation of Ohm's law keeping in mind the convention regarding signs of E and i. Ohm's law is also based upon conservation of energy.
Example 1. A battery of e.m.f. 6 volt and internal resistance 5 ohm is joined in parallel with another of e.m.f. 10 volts and internal resistance 1 ohm and combination is used to send a current through an external resistance of 12 ohm. Calculate the current through each battery.
Solution.
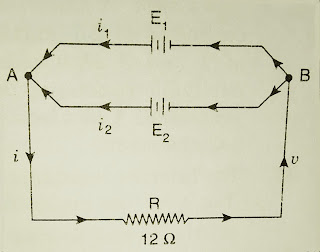 |
| Fig. 5. |
Example 2. A cell of e.m.f. 2 volt and internal resistance 1 ohm is connected with two wires of resistances 2 and 5 ohm in parallel. Find the current through each wire.
Solution.
 |
| Fig. 6. |




No comments:
Post a Comment