Resistance

 Resistance:

If  'V' be the potential difference between the two terminals of a conductor and 'i' be the current through it,then,

          V/i = Constant =R

'R' is called the resistance of the material

         i = V/R

An increase in the value of R results in a decrease in the value of  'i'.

Qualitative definition:

Resistance is the opposition offered by conductor to the flow of  electricity through it.Its value is given by equation R = ρ l/A.

Quantitative definition:

Resistance of a conductor is defined as the ratio between potential difference between the two ends of the conductor to the current flowing through it.

If          i = 1, R = V

resistance of a conductor can also be defined as the difference of potential across the two ends of the  conductor required to pass a unit electric current through it.

Concept of resistance:

Every  conductor contains a large number of free electrons. When a difference of potential applied between the two ends of the conductor, an electric field is set up inside the material of the conductor. A free electron (being a negatively charged particle) experiences a force, due to this field, which accelerates it from higher to lower potential side. After acquiring some velocity it suffers collision with other free electrons of the material and  loses the acquired energy. It, again, it accelerated and goes through the above process repeatedly. Thus, motion of the electron cannot be termed as free. It experiences resistance forward motion. This resistance is termed as electrical resistance.

Important notes:

Resistance of a conductor

1. is directly proportional to its length.
2. is inversely  proportional to its area of cross-section.
3. depends upon the nature of material i.e., on the number of electrons per meter cube of the material.
4. varies inversely on relaxation time τ. Since τ varies due to a variation a temperature, resistance is also varies with temperature.

Units of R:

(i) In S.I.

Unit of resistance in S.I. is 'ohm'

         1 ohm = 1 volt/ 1 ampere

resistance of a conductor is said to be 'ohm' if a current of one ampere flows through it for a potential difference of 1 volt across its end.

(ii) In C.G.S. system

     There are two types of unit in C.G.S. system. 

(a) e.s.u. of resistance or 'statohm'

         1 statohm = 1 statvolt/1 statamp

Resistance of a conductor is said to be 1 statohm if a current of 1 statampere flows through it for a potential difference of 1 statvolt across its ends.

(b) e.m.u. of resistance or 'abohm'

        1 abohm = 1 abvolt/1 abampere

Resistance of a conductor is said to be 1 abohm if a current of 1 abampere flows through it for a potential difference of 1 abvolt across its ends.

Dimension of R:

     [R] = potential difference/current

           = Work/charge /Current

           = [M1 L2 T-2]/[A1 T1] × [A1]

           = [M1 L2 T-3 A-2]

So, the dimension of resistance are 1, 2, -3 and -2, in mass, length, time and electric current respectively. 

Relation between ohm and statohm 

     1 ohm = 1 volt/1 ampere

                 = 1/300 statvolt/ 3 × 10⁹ statamp

∴   1 ohm = 1/ 9 × 10¹¹ statohm. 

Relation between ohm and abohm

     1 ohm = 1 volt/1 ampere

                 = 10⁸ abvolt / 1/10 abamp

     1 ohm = 10⁹ abohm

Variation of resistance with temperature:

Resistance R of a conductor is given by

     R = ml/ne²Aτ

As temperature of conductor increased, its free electrons absorb energy and become more vigorous. They shall, now undergo collisions more frequently, thus, resulting in a decrease of time of relaxation τ. Decrease in value of τ results in increase in the value of R. So, resistance of a conductor increase with an increase in temperature. Let 'R₀' and 'Rt' are its resistance at 0⁰C and t⁰C, respectively, then

         Rt = R₀ (1 + ∝t) 

         Rt = R₀ + R₀ ∝t

         R₀ ∝t = Rt - R₀

          ∝ = Rt - R₀/ R₀ t     ... (1) 

'∝' is known as temperature coefficient of resistance. 

Temperature coefficient of resistance is defined as change in resistance of the conductor per unit resistance per degree centigrade rise of temperature. 

Its S.I. unit is C-1.

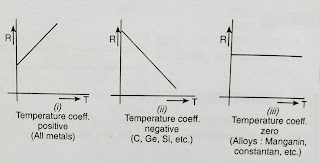
(i) For all metals and foe most of alloys '∝' is positive, i.e., their resistance increases with an increase in their temperature. 

    In Fig. 1(i), Rt - R₀ = BC,  R₀ = OA and t = AC

Substituting these values in equation (1) 

     ∝ = BC/OA × AC

       = BC/AC / OA 

       = tan ፀ/ OA

       = slope of the line/intercept on R-axis

Value of '∝' is greater for metals and smaller for alloys. Therefore metals show more change in resistance, as compared to alloys, when they are heated. This is the basic reason why alloys are used in resistance boxes and metals are used in the construction of resistance thermometers. 

(ii) Substances like carbon and semi-conductors possess negative value of '∝'. Their resistance decreases with a rise in temperature [Fig. 1(ii)]. 

(iii) There are certain alloys like manganin, constantan etc. Which do not show appreciable variation of resistance with temperature. Their temperature coefficient is zero. Variation of R with T is shown in [Fig.1 (iii)]. Hence resistance of such alloys does not change with  change in temperature. 

Fig. 1.

Colour Code for Resistances:

Wires made up of alloys can provide resistance of medium value. For very high resistances if the order of megohm we use carbon. The resistance of the piece is marked over it in the form of a code called colour code. Following two types of colour codes are used. 

(i) In one system there bands of colours on one end while there is a ring on the other end [in Fig. 2]. First band gives the first significant figure of resistance, second band gives the second significant figure while the third determines the number of zeros to be at the end. The colour code is follows. 

Black - 0

Brown - 1

Red - 2

Orange - 3 

Yellow - 4 

Green -5

Blue - 6

Violet - 7

Gray - 8

White -9

Fig. 2. Colour code for resistances. 

The ring at  the second end determines the percentage accuracy or reliability as per following rule:

Silver - ± 10%

Good - ± 5%

Example. Consider a carbon resistance marked with colour code with the three strips of colours - blue, red and orange respectively. It has a silver ring at the other end.

(I)                  (II)                  (III)              (R) 

Blue            Red               Orange        Silver

  6                   2                  (000)          (±10%) 

This is a resistance of 62,000 ohm with a tolerance of ±10% (silver ring) 

(ii) In the second system [in Fig. 3]  the body of the resistance is given one colour, the ends are given another colour while a dot (・) is marked over the body. A ring (silver or gold) on one side determines its tolerance. The colour code is same as described above. Colour of the body gives first significant figure, end colour gives the second significant figure while the dot determines the number of zeros at the end. The rings as usual determines the percentage tolerance. 

Fig. 3. Colour code for resistances. 

Illustration. [in Fig. 3], a resistance with green body, yellow ends and red dot is shown. 

(Body)          (Ends)            (Dot)           (Ring)  

Green           Yellow            Red             Gold

    5                     4                  00                5%

This is a resistance of 5,400 ohm with +5% tolerance. 

Important Notes:

1. Resistance of a conductor is directly proportional to its length. 
2. Resistance of a conductor is inversely proportional to its area of cross-section. 
3. Resistance of a conductor depends upon the nature of material i.e., on the number of electrons per meter cube of the material. 
4. It is varies inversely on relaxation time τ. Since τ varies due to a variation in temperature, resistance also varies with temperature.
5. Resistance and conductance are inverse of each other. 

Resistances in Series:

The resistances are said to be connected in series if same current flows through all of them. Consider resistances r₁, r₂ and r₃ connected in series with each other (Fiɡ. 4).

Fig.4. Resistances in series. 

  

 Let a current 'i' flows through all of them. If V₁, V₂ and V₃ are difference of potentials.

         V₁ = ir₁, V₂ = ir₂, and V₃ = ir₃ 

across each resistance, R is the resistance of combination, total potential difference 'V' across whole of the combination is

                     V = iR

Since           V = V₁ + V₂ + V₃

∴                 iR = ir₁ + ir₂ + ir₃

or               iR = i (r₁ + r₂ + r₃)

or                R = r₁ + r₂ + r₃

Thus, if a number of resistances are connected in series with each other, the net resistance of the combination is equal to the sum of their individual resistances. 

For series combination of n similar resistors the effective resistance

                   R₃ = Σ Ri  

  i

Resistances in Parallel:

Resistances are said to be connected in parallel if different currents flowing through them and get added afterwards. Consider a number of resistances r₁, r₂ and r₃ connected parallel to each other. A current i is divided into three parts and flowing through each of these resistances (Fig. 5). If 'V' is the difference of potentials across the combination, then

              V = ir₁ = ir₂ = ir₃

or          i₁ = V/r₁, i₂ = V/r₂, i₃ = V/r₃

Fig. 5. Resistances in parallel. 

If R is the resistance of the combination, then

                     i = V/R

Since           i = i₁ + i₂ + i₃

∴             V/R = V/r₁ + V/r₂ + V/r₃

or           V/R = V (1/r₁ + 1/r₂ + 1/r₃) 

               1/R = 1/r₁ + 1/r₂ + 1/r₃

Thus, if a number of resistances are connected in parallel, the reciprocal of the resistance of the combination is equal to the sum of reciprocals of their individual resistances. 

Resistances in Mixed Grouping:

Fig. 6 shows the mixed grouping of similar resistances each of value 'r'. 'n' resistances are connected in series in one row and there are m such rows (Fig. 6). All the 'm' rows are connected in parallel with each other across A and B. 

Fig. 6. Mixed grouping of resistances. 

Resistances of one row, 

R₁ = r + r + .... n times = nr

If R is the resistance of the combination, in which m resistance (each of value nr) are connected in parallel, 

           1/R = 1/nr + 1/nr + .... m

or       1/R = m/nr

or          R = nr/m

Net resistance = resistance × number of resistance in one row/number of rows