Electric Lines of Force and its Properties

Electric Lines of Force:

On account of electric intensity at all points in an electric field, unit positive charge will be urged to move in a definite direction when placed in the electric field. The path described by the unit positive charge is called the lines of force. 

      An electric lines of force is defined as the path, straight or curved, along which a unit positive charge is urged to move when free to do so in an electric field. The direction motion of unit positive charge gives the direction of lines of force. 

      The lines of force are straight if the electric field is due to an isolated charge and are curved if the field is due to two or more charges placed near each other. 

      Thus, a line of force may also be defined as a curve, tangent at any point of which gives the direction of the electric intensity at that point. 

Properties of Lines of Force:

1) The lines of force are directed away from a positive charge and are directed towards a negativity charge. 

      When a unit positive charge is placed near an isolated positively charged conductor, it gets repelled. Therefore, the lines of force, in this case, are directed away from the conductor. Fig. 1(i) shows the field lines due to a positively charged spherical conductor. These are directed radially outwards, i.e., along outward drawn normals. These lines are supposed to end at infinity. 

Fig. 1. Lines of force of isolated charges. 

      When, however, a unit positive charge is placed near an isolated negatively charged conductor, it gets attracted. Therefore, the lines of force, in this case, are directed towards the conductor. Fig. 1(ii) shows the field lines due to a negatively charged spherical conductor. These are directed radially inwards, i.e., alongward drawn normals. 

      Since, lines of force starts from positive charge and ends at negative charge, they are directed from higher potential to lower potential side. 

2) Tangent at any point on the lines of force gives the direction of electric intensity at that point [Fig.2].

Fig. 2. Direction of intensity at any point, on a lines of force. 

3) Two electric lines of force never intersect each other. 

      Let us suppose that two lines of force AB and A'B' intersect each other at a point P [Fig.3]. 

Fig. 3. Two lines of force intersecting each other. 

Since point P is common to both the lines of force, we can draw two tangents and P. Thus, there will be possibility of two electric intensities Ē1 and Ē2 at that point. Obviously, this is not possible. Hence two electric lines of force can never intersect each other. 

4) The number of lines of force per unit area (area being normal to lines) is proportional to magnitude of Ē. Thus, more concentration of lines represents stronger electric field. 

5) The lines of force tend to contract longitudinally or lengthwise, i.e., they possess longitudinally tension as shown in Fig. 4. Due to this property the two unlike charges attract each other. 

Fig. 4. Longitudinal contraction of electric lines of force. 

6) The lines of force tend to exert lateral (sidewise) pressure, i.e., they repel one another laterally. This explains the repulsion between two like charges in [Fig. 5].

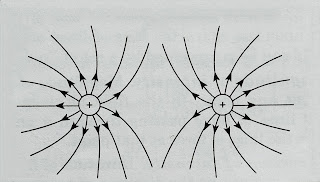Fig. 5. Lateral pressure of electric lines of force. 

7) The lines of force meet the surface of a spherical conductor normally. If it were not so, the electric field E will have a component (E sin θ) parallel to the surface of the conductor [Fig. 6]. This would mean a flow of current which is absurd. 

Fig. 6. If lines of force perpendicular to the surface of conductor. 

Because of this characteristic the electric field due to a charged conductor varies with a variation in the shape of conductor. Electric field due to a charged spherical conductor [Fig. 7(i)], pear shaped conductor [Fig. 7(ii)] are due to a flat sheet [Fig. 7(iii)] and shown here. 

Fig. 7. Effect of shape of conductor on field. 

8) Lines of force never pass through a conductor. This explains that there shall be no strength of electric field inside a conductor. This characteristic is used to build an electrostatic shield. Any charged body placed inside a metallic conductor shall be safe from any outside electrostatic field. 

9) The lines of force never pass through the conductor. This explains the absence of electric field within the conductor. 

10) One unit positive charge gives 4π lines of force in air. Thus, if the lines of force are crowded at a place, it indicates a strong field at that place. In the case of a weak field, the lines of force are far part. Parallel and equally spaced lined of force indicate uniform field.