Polar and non-polar molecule

Matter is composed of molecules which are neutral in spite of the charges contained in them. This is due to the reason that they contain equal and opposite charges. Positive charge (in the form of protons) is contained within the nucleus while the negative charge (in the form of electrons) is distributed all around it. A center of charge is a point where whole of the charge may be supposed to be concentrated for calculation purposes. Thus there will be two centers of charges; one for positive and the second for negative charges. 

Polar Molecule:

If the center of charge for positive and negative charges do not coincide, the molecule is equivalent to an electric dipole and is said to be a polar molecule. 

Such a molecule is associated with an electric dipole moment. When subjected to an electric field, the molecule experiences a torque and tends to fall in line with the direction of lines of force of the electric field [in Fig.1].

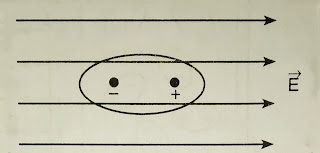Fig. 1. Polar molecule in electric. 

Non-polar Molecule:

 If the center of charges for positive and negative charges coincide, the molecule is said to be non-polar molecule [in Fig. 2(i)].

Such a molecule is not associated with an electric dipole moment. When subjected to electric field, there will be some relative displacement between the positive and negative charges. As a result, the center of charges for positive and negative charges will not remain coincident [Fig. 2(ii)].

Fig. 2. Non-polar molecule in electric field. 

Thus a non-polar molecule, when subjected to an electric field, acquires an electric dipole moment. 

Thus, polar and non-polar molecule behave in a similar manner when subjected to an electric field. 

Polarisation of the Di-electric:

A di-electric medium is always neutral whether it is made up of polar and non-polar molecules. The molecules are arranged at random. In case of polar molecules, the end of one having positive charge lies near the end of the other having negative charge [Fig.3(i)], thus neutralising each other's effect. Let this medium ne placed in between the two plates P and Q of a capacitor         [Fig. 3(ii)]. The electric field 'E' in between the plates exerts a torque on each of the dipole and tends to bring it along its lines of force. Greater the strength of the field, greater is the torque and and hence more is the number of dipole which get aligned along the lines of force. [Fig. 3(ii)] shows that all the dipoles have aligned themselves along the lines of force. In this stage the medium is said to be polarised. It will be observed that the two opposite forces of the di-electric acquire positive and negative charges and the medium is said to be polarised. This is due to the reason that the charges in between two dotted lines AB and CD neutralise each other's effect thus inducing negative charge on the left face and positive charge on the right face of the di-electric. 

Fig. 3. A slab of di-electric in an electric field. 

A quantitative measurement of polarisation of di-electric is done by polarisation vector P. 

Polarisation vector is defined as the electric dipole moment per unit volume of the material when placed in an electric field. 

            P = nP

Here vector P is the electric dipole moment of a molecule and 'n' is the number of molecules per cm³.

Units of P:

           [P] = A¹T¹/L² = C/m² = Cm-2

Unit of P in S.I. is Cm-2

Dimension of P:

      [P] = dipole moment/volume

            = charge × distance/distance³

      [P] = [A¹T¹] × [L]/[L³] = [L-2T¹A¹]

∴    [P] = [M0L-2T¹A¹]

Thus, dimensions of polarisation vector are 0, -2, 1, and 1 in mass, length, time and electric current, respectively. 

Polarisation vector and charge density. 

Let 'qi' be amount of charge induced on either face of the di-electric. 

Net electric dipole moment = qi × d

Where, 'd' is separation between two faces. 

∴   P = net electric dipole moment/volume

         = qi × d/a × d = qi/a

Where, 'a' is the area of cross-section. 

     But      qi/a = σi

Where, σi is the surface charge density of induced charge. 

∴            P =σi

Polarisation vector P varies directly as the strength of electric field E inside di-electric. 

            P ∝ E

or     P = constant × E

It can be shown that P has same dimensions as ε₀ E, therefore, the constant in this relation is replaced by χ  ε₀ E, where χ is a dimensionless constant depending on the nature of material. 

∴          P = χ ε₀ E

            P = [M0L-2T¹A¹]

           ε₀ = [M-1L-3T⁴A²]

          [E] = F/q = [M¹L¹T-2]/[A¹T¹]

               = [M¹L¹T-3A-1]

∴     [ε₀E] = [M-1L-3T⁴A²] × [M¹L¹T-3A-1]

                = [M0L-2T¹A¹]

χ is called the electric susceptibility of the 

material and is a measure how easily a material can be polarised.