Polar and non-polar molecule

Matter is composed of molecules which are neutral in spite of the charges contained in them. This is due to the reason that they contain equal and opposite charges. Positive charge (in the form of protons) is contained within the nucleus while the negative charge (in the form of electrons) is distributed all around it. A center of charge is a point where whole of the charge may be supposed to be concentrated for calculation purposes. Thus there will be two centers of charges; one for positive and the second for negative charges. 

Polar Molecule:

If the center of charge for positive and negative charges do not coincide, the molecule is equivalent to an electric dipole and is said to be a polar molecule. 

Such a molecule is associated with an electric dipole moment. When subjected to an electric field, the molecule experiences a torque and tends to fall in line with the direction of lines of force of the electric field [in Fig.1].

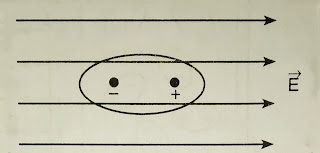Fig. 1. Polar molecule in electric. 

Non-polar Molecule:

 If the center of charges for positive and negative charges coincide, the molecule is said to be non-polar molecule [in Fig. 2(i)].

Such a molecule is not associated with an electric dipole moment. When subjected to electric field, there will be some relative displacement between the positive and negative charges. As a result, the center of charges for positive and negative charges will not remain coincident [Fig. 2(ii)].

Fig. 2. Non-polar molecule in electric field. 

Thus a non-polar molecule, when subjected to an electric field, acquires an electric dipole moment. 

Thus, polar and non-polar molecule behave in a similar manner when subjected to an electric field. 

Polarisation of the Di-electric:

A di-electric medium is always neutral whether it is made up of polar and non-polar molecules. The molecules are arranged at random. In case of polar molecules, the end of one having positive charge lies near the end of the other having negative charge [Fig.3(i)], thus neutralising each other's effect. Let this medium ne placed in between the two plates P and Q of a capacitor         [Fig. 3(ii)]. The electric field 'E' in between the plates exerts a torque on each of the dipole and tends to bring it along its lines of force. Greater the strength of the field, greater is the torque and and hence more is the number of dipole which get aligned along the lines of force. [Fig. 3(ii)] shows that all the dipoles have aligned themselves along the lines of force. In this stage the medium is said to be polarised. It will be observed that the two opposite forces of the di-electric acquire positive and negative charges and the medium is said to be polarised. This is due to the reason that the charges in between two dotted lines AB and CD neutralise each other's effect thus inducing negative charge on the left face and positive charge on the right face of the di-electric. 

Fig. 3. A slab of di-electric in an electric field. 

A quantitative measurement of polarisation of di-electric is done by polarisation vector P. 

Polarisation vector is defined as the electric dipole moment per unit volume of the material when placed in an electric field. 

            P = nP

Here vector P is the electric dipole moment of a molecule and 'n' is the number of molecules per cm³.

Units of P:

           [P] = A¹T¹/L² = C/m² = Cm-2

Unit of P in S.I. is Cm-2

Dimension of P:

      [P] = dipole moment/volume

            = charge × distance/distance³

      [P] = [A¹T¹] × [L]/[L³] = [L-2T¹A¹]

∴    [P] = [M0L-2T¹A¹]

Thus, dimensions of polarisation vector are 0, -2, 1, and 1 in mass, length, time and electric current, respectively. 

Polarisation vector and charge density. 

Let 'qi' be amount of charge induced on either face of the di-electric. 

Net electric dipole moment = qi × d

Where, 'd' is separation between two faces. 

∴   P = net electric dipole moment/volume

         = qi × d/a × d = qi/a

Where, 'a' is the area of cross-section. 

     But      qi/a = σi

Where, σi is the surface charge density of induced charge. 

∴            P =σi

Polarisation vector P varies directly as the strength of electric field E inside di-electric. 

            P ∝ E

or     P = constant × E

It can be shown that P has same dimensions as ε₀ E, therefore, the constant in this relation is replaced by χ  ε₀ E, where χ is a dimensionless constant depending on the nature of material. 

∴          P = χ ε₀ E

            P = [M0L-2T¹A¹]

           ε₀ = [M-1L-3T⁴A²]

          [E] = F/q = [M¹L¹T-2]/[A¹T¹]

               = [M¹L¹T-3A-1]

∴     [ε₀E] = [M-1L-3T⁴A²] × [M¹L¹T-3A-1]

                = [M0L-2T¹A¹]

χ is called the electric susceptibility of the 

material and is a measure how easily a material can be polarised. 

Conductor, Insulator (dielectric) and Semi-conductor

Conductor, Insulator and Semi-conductor:

An atom consists of a central positively charged core known as nucleus. The nucleus is surrounded by a number of electrons revolving around it in practically circular orbits. In some substances, the electrons in the outermost orbits are loosely bound to the nucleus. These electrons may leave the atom and become 'free electrons'. The motion of free electrons is random. Due to the motion of free electrons, charge is carried from one end of the substance to the other. In certain substances, the orbital electrons are strongly bound to the nucleus. In these substances, free electrons are available only in small number. So, charge cannot flow easily from one end of the substance to the other. Depending upon the capacity to allow the passage of charge, the substances are generally classified into three categories. 

1. Conductor

2. Insulator

3. Semi-conductor

1. Conductor. Conductor are those substance through which electric charge can pass easily. 

Example- Silver, Iron, Copper, Aluminium etc. 

Among metter silver is the best conductor of electricity. Conductor contain large number of free electron, due to the repulsion between free electron they get evenly scattered through out the conductor. Therefore, no portion of the conductor has accumulation of electrons (i.e., charges). 

2. Insulator. Insulator are those substance through which electric charge cannot pass easily. 

Example- Glass, Wood, Mica, Plastic, Rubber, Umber, Sulphur etc. 

Insulator contain a negligible number of free electron. 

If any region of the insulator happens to have an accumulation of electron they will remain localised in that region. 

But conductivity of any substance is effected by temperature on heating the insulator tends to become conductor.

3. Semi-conductor. The substance whose conductivity lies between conductor and insulator are called semi conductor. 

Example- Silicon (si), Germanium (G) are known as semi conductor. 

Semi conductor is covalent bond.

No substance is a perfect conductor or a perfect insulators. The difference between conductors and insulators is only of the degree. The insulating ability of fused quartz is about 10²⁵ times as great as that of copper. Thus, these materials behave as perfect insulators for many practical purposes. Under suitable conditions, both conductors and insulators can be electrified.

Conductors in an Electric Field:

(i) Field inside a conductor in an electric field. When an electron leaves an atom, the electron is known as free electron and the reminder atom is known as positive ion. In a conductor the number of free electrons is equal to the number of positive ions. 

Consider a conductor (of any shape) placed in a uniform electric field (strictly speaking, it is an electrostatic field). This field is produced by two oppositely charged plates A and B. Under the influence of this external field, the positive ions (in the conductor) will being to move in the direction of the field, i.e., along the electric lines of the force. The free electrons (in the conductor) are driven in the opposite direction, i.e., in a direction opposite to the electric lines of force. Both the positive ions and electrons cannot go beyond the surface of the conductor. This results in concentration of opposite charges at the two ends of the conductor. These charges set up their own electric field inside the conductor as shown in    [Fig. 1(i)]. This electric field tends to oppose that external electric field. The strength of the opposing field goes on increasing with the increase in concentration of charges increases at the surface of the conductor. The concentration of charges increases to such a value that their electric field exactly balances the external electric field. At this stage there will be an electric lines of force inside the conductor as shown in [Fig. 1(ii)]. This indicates that the electric field inside a conductor is zero. Because of the absence of electric field inside the conductor, all the points just below the surface of the conductor are at the same potential. 

Fig. 1. A conductor in uniform electric field. 

(ii) Electrostatic shielding. Consider an electric field produced by pair of two oppositely charged parallel plates P and Q [in Fig. 2]. The lines of force starts from the conductor at Higher potential and terminate on a conductor at lower potential. Therefore, there cannot be any lines of force between two conductors having same potential. 

Let a hollow conductor ABCD be placed inside the field. Since the surface of a conductor, whatever is shape may be, is always equipotential, therefore, there cannot be any line of force inside the conductor. Because in the event of a line of force being there, it would have started and then ended on two points at same potentials which is not possible.

Fig. 2. Electrostatic shielding. 

 The absence of lines of force inside a conductor indicates that no force is experience by buy any charge placed inside it, i.e., the charge inside a hollow conductor remains unaffected by a field outside it. In other words, the charge is shielded from the outside field. 

Similarly a charge placed inside the hollow conducting enclosure will not produce any effect outside it. 

The phenomenon of electrostatic shielding is employed extensively to protect very delicate instruments from any external charged particles. 

(iii) Charge resided inly on the surface. It can be proved, using Gauss's theorem, that a conductor having a static charge has whole of the charge residing on the surface of conductor. Consider a Gaussian surface as shown dotted in [Fig. 3], drawn in such a way that it lies very close to it and below it. 

Fig. 3. A conductor with static charges. 

Since E(r) everywhere is zero the flux through, this surface is zero. Applying Gauss's theorem it can be concluded that there is no charge inside the surface. This is possible only if whole of the charge is distributed over the surface. 

(iv) Field is always perpendicular to the surface. It can further be shown that the electric field, just outside the surface must be perpendicular to the surface at all points. Let 'E' be the direction of field, in general, at a point P, just outside a conductor C with static charges [Fig. 4]. Resolving E into two components, we get, 

• E cos θ along PX, acting perpendicular to the surface. 

• E sin θ along PY, acting tangential to the surface. 

Fig. 4. Electric field always perpendicular to surface of conductor. 

The tangential component 'E cos θ' can make the free electrons to drift continuously this, causing electric currents flowing in closed circuits. This is not possible in case if a conductor with static charge. Hence there cannot be any existence of 'E cos θ' meaning that the field should always be perpendicular to the surface. 

(v) Field strength at a point just outside the surface. According to Gauss's law, 

           ∫ E. ds = 1/ε₀ q 

E(r) being always perpendicular to the area, E and ds have same direction (θ = 0°) 

     ∫ E(r). dS = ∫ EdS = ∫ E dS = ES

Using Gauss's theorem, we get                                                 ES = 1/ε₀ q

It σ us surface charge density,   q = σS

∴      ES = 1/ε₀ (σS)    or    E = σ/ε₀

 

This gives magnitude of the field strength. 

(vi) Conductor containing a charge in a cavity inside it. Consider an uncharged conductor having a cavity in it containing a charge +q at O [Fig.5].

Fig. 5. Charge located in a cavity inside a conductor. 

Let there be a Guassian surfaces as shown dotted. 

According to the Gauss's theorem, 

     ∫ E(r). dS = 1/ε₀ Σq

Where  'Σq' is the total charge located inside the surface. 

Since E in the conductor is zero, 

∴      Σq = 0

Since we know that a charge +q is located at O, Σq = 0 only if there is charge -q on the inside of the cavity. For the conductor to be neutral, a charge +q will have to be there on the surface. This is again an evidence in the support of fact that the charge resides on the outer surface. 

Insulator in an Electric Field:

An insulator has no free electrons and thus no motion of charge carries takes place when it is placed in an electric field. However, when it is placed in a strong electric field, the orbits of the atoms of the insulator and stretched which results in the separation of centers of negative and positive charges. The atom is said to be polarised. The polarised charges in the surface of insulator produce an electric field which decreases the resultant electric field inside the insulator. 

Relation between electric field and potential difference

Relation between Electric Field and Potential Difference:

Consider an arbitrary curve AB in a non-uniform electric field [in Fig]. Let P be any point on this curve. We know that this potential difference between A and B is equal to the negative line integral of field strength from A to B. 

Motion of a point charge in a non-uniform electric field. 

∴     V(rB) - V(rA) = - BA∫ E(r) . dl

If the point A is removed to infinity, potential at any point is given by

        V(r) = - r∞∫ E(r). dl

Let Q be another point situated very close to P at a very small distance 'dl', so that the field between P and Q is practically the same. In that case the potential difference 'dV' between these points can be written as

      dV = - E. dl

            = - E dl cos θ

Where  'θ' is the angle between E and dl

∴      dV = - E cos θ dl      or     dV = - ET dl

Where  represents the tangential component of E along dl. 

∴     ET = - dV/dl

Here, -dV/dl denotes the rate of change of potential along a line and is known as the potential gradient. 

Therefore, the component of electric intensity, along any direction is equal to the negative potential gradient in that particular direction. 

The negative sign in equation ET = - dV/dl indicates that the direction of E coincides with that of decreasing potential. 

Electric potential

Electric Potential:

An analogy. Consider two tubes A and B [in Fig.] Containing water and isolated from each other through a stop clock S. Amount of water in A is much less than in B while the level of water in A is higher than that in B. On opening stop clock it will be observed that water flows from higher level to lower one (i.e., from A to B) till the level becomes equal in two tubes. Thus, the factor that determines the direction of flow of water is the level of water and not the amount of water. Similarly in heat the factor that determines flow of heat from one body to the other is the temperature and not the amount of heat contained in the body. 

Fig. 1. Motion of water from a higher level to a lower level. 

     Correspondingly, in electricity, there is a quantity which determines the direction of flow of charge from one body to the other irrespective of the amounts of charges contained in the two bodies. This quantity is called electric potential of the body. Charges flows from a body at higher potential to that at a lower potential. 

Qualitative definition:

     Qualitatively, electric potential may be defined as the quantity which determines the direction of flow of charge between two bodies. 

In equation, V(rB) - V(rA) = - BA∫ E(r). dl     ..... (1), we have seen that negative line integral of electric field between any two points is equal to the difference between the values of scalar function V for two points rA and rB  . It is always convenient for us to choose this scalar function so that its value at infinite distance from the source of electric field is zero. Let the point rA  be removed to infinity. 

     ∴          V(rA) = 0

     So equation (i) can be written as

         

          V(r) = - ∞r∫ E(r). dl ...... (2)

     It may be noted that we have dropped the subscript 'B' here since it has become meaningless now. 

     Equation (2) defines the potential at a    point r. 

Quantitative definition:

     Electric potential at any point, is defined as the negative line integral of electric field from infinity to that point along any path. 

Potential difference:

     Using this concept, equation (2) defines the potential difference between any two points in the electric field. 

     Potential difference, between any two points, in an electric field is the negative line integral of electric field between them along any curve joining them together. 

Physical concept:

     Consider a small charge 'δq' being brought from infinity to a point r against an electric field of strength E(r'). Force F(r') acting on the charge δq while at a point r' is given by

           F(r') = δq E(r') 

     Since we have to push the charge against electric field we shall have to do work upon it. Thus, the potential energy of the charge will increase. Let this increase in potential energy be 'dW' when pushed through a small distance dl. 

               dW = - F(r'). dl

     Substituting for F(r')  dW = δq E(r'). dl

     If W is the work done in moving 'δq' from infinity to the point r', 

        W = W∞∫ dW = - δq ∞r∫ E(r'). dl ...... (3)

or

        W = δq. V(r)        [∵  - ∞r∫ E(r'). dl = V(r)]

 ∴   ∴        V(r) = W/δq                           ...... (4) 

If        δq = 1, V(r) = W. 

     Thus, potential, at any point, in an electric field, is defined as the work done in moving a unit positive charge from infinity to that point against the electric field along any path. 

Potential difference:

     If equation (3) is evaluated between two points rA  and rB , work done WAB  in that case is given by 

          V(rB) - V(rA) = WAB/δq

     In case of conservative field

      

           F = - dU/dx    or    dU = - Fdx

or

      Increase in potential energy = - (work done upon it) 

     If   δq = 1,      V(rB) - V(rA) = WAB.

     Potential difference, between any two points, in an electric field is defined as the work done in taking a unit positive charge from one point to the other against the electric field 

Units of Potential or Potential Difference:

(i) In S.I. units

       Unit of potential, in S.I. is volt (V) 

       If           δq = 1 C and W = 1 J

       Using equation (4),    

                  V(r) = 1 J/1 C = 1 volt. 

     Potential at any point, in an electric field, is said to be 1 volt if if 1 joule of work is done in moving a charge of 1 Coulomb between infinity to that point against the electric field along any path. 

(ii) In C.G.S. system:

      There are two types of units for potential in C.G.S. system. 

(a) e.s.u. of potential or statvolt

   1 e.s.u. of potential = 1 erg/1 e.s.u. of charge

     Potential, at any point is said to be 1 e.s.u. of potential or one statvolt of 1 erg of work is done in moving a charge of 1 e.s.u. between infinity to that point against the electric field along any path. 

(b) e.m.u. of potential or abvolt   

 

         1 e.m.u. of potential=1 erg/1 e.m.u. of charge

     Potential at any point, is said to be 1 e.m.u. of potential or 1 abvolt  if 1 erg of work is done in moving q charge of 1 e.m.u. between infinity to that point against the electric field along any path. 

Relation between volt and statvolt

          1 volt = 1 joule/1 coulomb

                     = 10⁷/3 × 10⁹ statcoulomb

∴        1 volt = 1/300 statvolt.

Relation between volt and abvolt

   

               1 volt = 1 joule/1 coulomb

                          = 10⁷ erɡ/1/10 abcoulomb               ∴        1 volt = 10⁸ abvolt

     It may be noted that abvolt is the smallest unit of potential while statvolt is the biɡɡest unit.

Relation between statvolt and abvolt

               1/300 statvolt = 10⁸ abvolt

    ∴         1 statvolt = 3 × 10¹⁰ abvolt

Electric potential at any point due to a single point charge

Electric potential at any point in an electric field is defined as the amount of work done in moving a unit positive charge between infinity to that point without any acceleration against the electric force. 

     If the source charge is positive, unit positive charge is moved from infinity to that point while in case of negative source charge, unit positive charge is taken from the given point to infinity. 

Case (i) Source charge situated at the origin

     Let the source charge q be situated at O. We intend to determine electric potential at Practice, distant r from O. Imagine moving unit positive charge from infinity towards People (Fig. 2). At any instant, during this process let the charge be at A, distant x from O. 

Fig. 2. Source charge at origin. 

     Let E (rightward arrow) be the electric intensity (force acting on a unit positive charge) at A. Small amount of work dW done to move the unit charge from A to B is 

           dW = E . dx = E dx cos 180° (E . dx is in right ward arrow) 

or          dW = - E dx 

     But      E = 1/4πε₀ × q/x²

     ∴      dW = - 1/4πε₀ × q/x² × dx          ... (5) 

     Net work done in moving the charge from infinity to P is

W = W0∫ dW = - q/4πε₀ r∞∫1/x² dx 

               = - q/4πε₀ r∞∫ x-2 dx

               = q/4πε₀ [x-2 +1/-2 + 1]r∞ 

               = - q/4πε₀ [x-1/-1]r∞

           W = - q/4πε₀ [-1/x]r∞ 

               = - q/4πε₀ [(-1/r) - (-1/∞)]

or      W = q/4πε₀ × 1/r

     According to the definition of electric potential V. 

                      V = W

∴                    V = q/4πε₀ × 1/r                ... (6) 

     Potential at any point is a scalar quantity (being the work done per unit charge). It is positive for a positive source and negative for a negative source charge. 

     Potential difference between two points A and B in the electric field will be

          VB - VA = q/4πε₀ × [1/| rA | - 1/r]

where rA and rB (both rA and rB is in rightward arrow) are the position vectors of A and B respectively. 

Case (ii) Source charge situated anywhere

Let r' (rightward arrow) be the position vector of source charge (Fig. 3).

Fig. 3. Source at any point. 

     According to triangle's law, 

                      SP = OP - OS  (SP, OP, OS are in rightward arrow) 

     ∴               SP = r - r'  (SP, r, r' are in rightward arrow) 

     Potential at P, in this case is given by

            V = 1/4πε₀ × q/|SP|

or     V = 1/4πε₀ × q/|r - r'|

     Potential difference between two points A and B will be 

            VB - VA = q/4πε₀ [1/| r - r' | - 1/| rA - r' |

where rA and rB (both rA and rB is in rightward arrow) are the position vectors of A and B respectively. 

Potential difference between two points

Potential difference between two points in an electric field is defined as the amount of work done in moving a unit positive charge from one point to the other, without any acceleration against the electric force. 

Case (i) Source charge situated at the origin

     Net work done in moving a  unit positive charge A to B (Fig. 3) can be obtained by integration equation (5) between the limits x = rA to x = rB. 

WAB = WAB0∫ dW = q/4πε₀ rBrA∫ 1/x² × dx

        = - q/4πε₀ [x-2 + 1/-2 + 1]rBrA

        = - q/4πε₀ [(- 1/rB) - (- 1/rA)]                       or        WAB = q/4πε₀ (1/rB - 1/rA) ... (7)

Fig. 4. Source charge at origin. 

     Equation (6), can be obtained from this by substituting rA = ∞ and rB = r. 

Case (ii) Source charge situated anywhere

     In case the source charge 'q' is situated at S [r' (rightward arrow)] (Fig. 5), the potential difference between two points A (rA) and B (rB) is given by

VB - VA = 1/4πε₀ [1/| SB | - 1/| SA | (SB and SA is in rightward arrow)

or    VB - VA = 1/4πε₀ [1/| rB - r' | - 1/| rA - r' |] (rB - r' and rA - r' is in rightward arrow)

Fig. 5. Source charge at anywhere. 

Potential Energy of a charge

We know that electric field exits at all the points around a source charge q' and every point is characterised with electric potential (work done in bringing a unit positive charge from infinity to that point) which is given by

             V(r) = 1/4πε₀ × q'/r

     If instead of bringing a unit charge , we bring a charge 'q' from infinity to that point, work done 'W' in doing so is given by

             W = q × V(r) (r is in rightward arrow) 

or         W = 1/4πε₀ × qq'/r

     This work done is termed as the potential energy of the charge q in the field of charge q'. 

     (i) If q and q' are of same nature, potential energy is positive. This is due to the repulsive force between them. 

    (ii) If q and q' are of opposite nature, potential energy is negative. This is due to the attractive force between them. 

     Thus, we can also say that the electric potential at any point in an electric field is numerically equal to the potential energy of a unit positive charge placed at that point. 

Important notes

(i) Electric potential is analogous to height in mechanics and temperature in beat.  (ii) Electric potential is a scalar quantity.  (iii) It is the negative line integral of electric field between infinity and the given point.  (iv) Electric potential at any point varies inversely as the distance of the point from source charge.  (v) Electric potential at any point due to a positive charge is positive while that due to a negative charge is negative.